アイテムを全コンプするのに必要なガチャ回数の期待値を計算するアプリを作りました。
内部ではシミュレーションや近似等は行っておらず、厳密な期待値が計算可能な手法を採用しています。
この記事では、この手法に関して以下の流れで解説していきます:
- 問題モデル化
- 数式を使った解析
- 数値計算に落とし込む
この記事の構成
この記事は以下のようなパートから構成されています:
問題のモデル化:
数式を使った解析:
数値計算に落とし込む:
このアプリを作るまでの流れ/経緯
話の本筋とは関係ないですが、このアプリを作った経緯は以下のようになります:
プランナーさんがガチャを企画していて、適当な確率配分を探るために、アイテム全取得のために必要なガチャの回数の期待値が計算できると嬉しい(要約)という依頼が来た。→ 計算できるコードを書いた。
せっかくなので、誰でも使える形で公開しよう(ついでアルゴリズムも改良しコードも大幅に書き直して…)→ できたものがコレ
また、今回どうして解説記事を書こうと思ったかというと、このアプリを作る上で使った道具群、特にマルコフ連鎖は基本的であると同時に応用上も非常に重要で、応用数学や数値計算のネタ(入門)の題材としてはわりと良いんじゃないかなと感じたからです。
ガチャを数学的にどう表現するか
まずガチャの問題をどう定式化し、どのような数理モデル(数式表現)に当てはめるのかを考えます。
ガチャでアイテムをコンプするとは?
ガチャではクジを回してアイテムを集めていきます。毎回クジを引くごとに、複数種類の中からアイテムを一つ貰えます。アイテムをコンプするとは、くじを引き続け、全種類のアイテムを取得する事です。
具体的には毎回クジを引くごとに、\(I\)種類のアイテム\([1, \ldots, i ,\ldots, I]\)の中から一つのアイテム\(i\)を確率\(p(i) > 0\)で取得していきます。
ちなみに\(p(i)\)が互いにすべて等しい場合はCoupon collector’s problemと呼ばれ、アイテムを全て取得するのに必要なクジを引く回数の期待値は\(I\sum_{n=1}^I1/n\)であることが知られています。
ガチャを表現する数学的モデル
ガチャの問題を記述するもっとも適当なモデルはマルコフ連鎖です。マルコフ連鎖とはマルコフ過程の一種であり、マルコフ過程は確率過程の一種です。まず確率過程の説明からしていきます。
確率過程(離散時間上での)とは、各時刻(ステップ)ごとに、状態が確率的に変化していくような対象の数学的なモデルです。確率過程は確率分布の一種であり、時刻(ステップ数)を表す添字\(t \in \mathbb{N}\)のついた確率変数\(X_{t}\)を用いて、 $$ P(X_0=x_0, X_1=x_1, \cdots, X_t=x_t , \cdots) $$ として表現されます。ここで\(x_{t} \in \mathbb{S}\)は確率変数\(X_t\)の実現値であり、\(\mathbb{S}\)は状態全体の集合を指します。
マルコフ過程とは、次の時刻にどの状態に移るかの確率が現時刻での状態にのみに依存するような確率過程を指します。これは数式を使うと、以下のように左辺のような条件付き確率が右辺のような条件付き確率として書き表せることに相当します: $$P(X_{t}=x_t|X_{t-1}=x_{t-1} , \cdots, X_{0}=x_{0}) = P(X_{t}=x_t|X_{t-1}=x_{t-1}).$$ マルコフ連鎖とは、状態の集合\(\mathbb{S}\)が有限集合(一般には可算集合)の場合を指します。マルコフ連鎖は遷移行列\(R\)によってパラメトライズ(=モデルを記述)することができます。
ここで遷移行列\(R=[r_{su}]\)とは、各ステップで状態\(s \in \mathbb{S}\)から状態\(u \in \mathbb{S}\)へ遷移する確率\(P(X_{t+1}=u|X_t=s)=r_{su}\)を行列の形で並べたものです。マルコフ連鎖は数学的に扱いやすく(=線形代数と相性が良く)、様々な分野への応用があります。
マルコフ連鎖は以下のような状態遷移図の形で表現されることもあります:
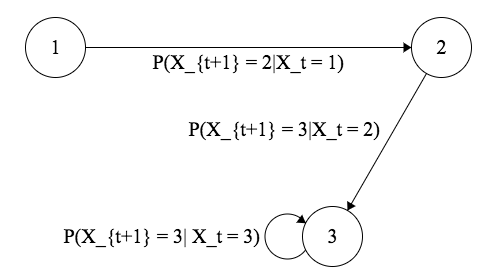
ここで各ノードが状態を表し、各エッジに割り振られた値が状態間の遷移確率を表します。マルコフ性により、次にどの状態に遷移するかの確率が、これまで辿ってきた状態の履歴に依らず今いる状態のみによって決定されるためこのような表現が可能となります。
マルコフ連鎖をガチャの問題に当てはめると、それぞれの文字はこのように対応します: \(X_t\)がガチャを\(t\)回引いた後でのアイテムの所持状態の確率変数、\(x_t\)がその実現値、\(\mathbb{S}\)がアイテムの所持状態の全体の集合、\(R_{su}\)がガチャを一回引いた時のアイテムの所持状態\(s\)から\(u\)への遷移確率となります。
マルコフ連鎖の特徴と応用
マルコフ連鎖の数学的特徴
マルコフ連鎖の数学的に嬉しい所は線形代数との相性が良い点です:
- 状態の確率分布(\(\pi_t\))の時間発展を、遷移行列の積を使って表現できる: \(\pi_t = \pi_0 R^t\)。これはチャップマン=コルモゴロフ方程式が行列の積として表現されることに相当する。
- 行列計算に関する学問である線形代数での豊富な道具/議論が使える。例えば定常分布\(\pi\)を固有値問題:\(\pi R= \pi\)を解くことで求めることができる。
マルコフ連鎖の応用事例
マルコフ連鎖はその扱いやすさからか様々な分野への応用があります:
待ち行列理論(数学者アーラン(プログラミング言語Erlangの名前の元ネタ)が開拓した分野)
- 元は交換機のある電話回線を記述するために作られた
- 今風な言い方をすると、キューに入ったタスクを捌き切るのに必要な、workerの個数や性能を数学的に解析できる
GoogleのPageRankアルゴリズム
ガチャの問題で状態空間と遷移行列をどう表現するか
ガチャの問題をマルコフ連鎖を使ってモデリングするには、その状態空間と遷移確率を具体的に与える必要があります。
状態空間\(\mathbb{S}\)の表現
ガチャにおいて各時刻での状態の集合(状態空間)\(\mathbb{S}\)を具体的にどう表現するかを考えます。
\(I\)種類のアイテム\([1, \ldots, i ,\ldots, I]\)を各ステップごとに1つずつ取得していくので、 各アイテムの所持数を並べたもの\((k_0, \cdots, k_i,\cdots, k_I), k_i \in \mathbb{N}\)をアイテムの所持状態として使うのが最も素朴なやり方ではあります。
しかしこの時、状態の集合\(\mathbb{S}=\{(k_0, \cdots, k_i,\cdots, k_I)\}\)は\(\mathbb{N}\)の\(I\)個の組み合わせ(=直積)\(\mathbb{N}^I\)となりますが、これは集合のサイズとしては無限(加算無限)であるため、この集合の上での確率分布を考えるのは計算機で数値的に取り扱うのが困難です。
なので代わりに、各アイテムを持っているか/いないかを表す変数\(h_i \in \{0, 1\}\)を並べたものでアイテムの所持状態を表現することを考えます。
\(h_i\)はアイテム\(i\)を所持していない(\(k_i=0\))時に\(0\)の値をとり、1つ以上所持している時(\(k_i > 0\))に\(1\)の値を取ります。このとき\(\mathbb{S} = \{(h_0, \cdots, h_i,\cdots, h_I)\} = \{0, 1\}^I\)となり、状態空間の大きさは\(|\mathbb{S}|=2^I\)となります。
遷移確率\(r_{su}\)の計算
状態\(s\)から状態\(u\)への遷移確率\(r_{su}=P(X_{t+1}=u|X_{t}=s)\)がどのような値になるかを考えます。 アイテムの所持状態の遷移は次の2パターンに分類されます:
(1) 新しい種類のアイテム\(i\)を取得する (2) 既に出たアイテムがドロップし(=ダブリ)、所持状態は変化しない。
状態\(s, u\)を具体的に\(s = (h^s_0, \cdots, h^s_i,\cdots, h^s_I)\)、\(u = (h^u_0, \cdots, h^u_i,\cdots, h^u_I)\)とした時に、(1)のパターンでの状態遷移\(s \to u\)は以下のような状況に相当します: $$ \begin{cases}
h^s_j=h^u_j & j \neq i,\\
h^s_j=0, h^u_j=1& j = i.
\end{cases} $$ このとき遷移確率\(r_{su}\)は $$ r_{su} = p(i) $$ となります。(2)の場合、つまり\(s=u\)の場合の遷移確率は、既に取得しているアイテムがドロップする確率なので $$ r_{ss} = P(X_{t+1}=s|X_{t}=s) = \sum_{i=1}^I h^s_ip(i) $$ となります。
(1)および(2)以外のケースでは遷移確率は\(0\)となります。これは例えば、一回のガチャで複数個のアイテムがドロップしたり、持ってるアイテムが消えたりするようなケースはありえないこと(=確率が\(0\))に対応しています。
状態空間を圧縮する
ここまでの議論で定義された状態空間だとその大きさ\(|\mathbb{S}|\)は\(2^I\)となっていますが、同一のドロップ確率のアイテムが複数ある場合には、空間の大きさを圧縮し、計算量を削減することができます。
同一のドロップ確率のアイテムが複数ある場合とは具体的にはアイテムにいくつかの種類のレア度があり、各レア度でのドロップ確率が等しいという様な状況をここでは指します。
レア度の存在するアイテムガチャの定義は以下のようになります:
まずレア度を\([1, \ldots,j \ldots, J]\)として、レア度\(j\)のアイテムの個数を\(M_j\)、ドロップ確率を\(p_{rare}(j)\)とします。ここで確率の総和は\(1\)なので\(\sum_{j=1}^JM_jp_{rare}(j)=1\)が成り立っています。
状態空間\(\mathbb{S}\)の表現は、同一レア度のアイテムは、ドロップ確率が等しく互いに区別する必要がないことから、「各レア度のアイテムを何種類持っているか」を表す量\(m_j \in [0, \ldots, M_j]\)を使って表現できます。
具体的には\(\mathbb{S}\)は\( [0, \ldots, M_j], j \in [1, \ldots,j \ldots, J]\)の直積になります: $$ \mathbb{S} = [0, \ldots, M_1] \times \cdots \times [0, \ldots, M_j] \times \cdots \times [0, \ldots, M_J]. $$ この新しい表現での状態空間のサイズは\(|\mathbb{S}|=\prod_{j=1}^J (M_j +1)\)となっています。
これは例えば、同一ドロップ確率のアイテムが10種類ある場合、元の状態空間の表現ではサイズが\(1024=2^{10}\)となってるものが、新しい表現だと\(11=10+1\)になっています。
遷移確率\(r_{su}\)は、元の(圧縮されてない)状態空間の場合と同様の考え方で計算することができます。
具体的には、\(m^s_j, m^u_j \in [0, \ldots , M_j]\)、\(s = (m^s_0, \cdots, m^s_j,\cdots, m^s_J)\)、\(u = (m^u_0, \cdots, m^u_j,\cdots, m^u_J)\)として $$ r_{su} =
\begin{cases}
1 – m^s_jp_{rare}(j)/M_j & [m^s_l = m^u_l (l\neq j), m^s_j +1 = m^u_j ], \\
\sum_{j=0}^j m^s_jp_{rare}(j)/M_j & m^s_j = m^u_j, \\
0 & \mbox{else}.
\end{cases} $$ となります。
状態空間\(\mathbb{S}\)を自然数にエンコードする関数\(\phi\)
\(r_{su}\)を行列の形で並べたものが遷移行列\(R\)ですが、「並べる」ためには状態空間\(\mathbb{S}\)を適当な全順序集合、例えば区間\(\mathbb{L} = [0, \ldots , |\mathbb{S}|-1]\)と一対一対応させる必要があります。この対応写像\(\phi^{-1}: \mathbb{S} \to \mathbb{L}\)を以下のように定義します: $$ \phi^{-1}(s) = \sum_{j=1}^J m^s_j \prod_{l=1}^{j-1} (M_l+1). $$ この定義は通常の基数を使った自然数の表現(\(M_j\)が互いにすべて等しい場合)の自然な拡張になっています。\(\phi^{-1}\)及びその逆写像\(\phi\)が一対一対応(全単射)になっていることは、\(\mathbb{L}\)と\(\mathbb{S}\)の集合サイズ(濃度)が等しいこと、\(\phi^{-1}(\mathbb{S}) \subseteq \mathbb{L}\)となっていること、\(\phi^{-1}\)の出力が重複しない(単射)なことから確認できます。
アイテムコンプの期待値の表現と計算
アイテムコンプに必要なガチャ回数の期待値を確率を使って計算/表現してみます。さらにその期待値表現を行列を使った計算に置き換えます。
期待値を計算してみる
\(c = (M_1, M_2, \cdots, M_J) \in \mathbb{S}\)をアイテムを全て取得している状態とします。\(T\)をアイテムコンプを達成した最初の時刻\(t\)を表す確率変数とすると、\([T=t] \leftrightarrow [X_{t}=c, X_{t-1}\neq c]\)が成り立つことから\(T\)の期待値\(S\)は以下のようになります: $$ S = E[T] = \sum_{t=1}^\infty t P(X_{t}=c, X_{t-1}\neq c). $$ \(S\)はさらに $$ S = \sum_{t=1}^\infty t P(X_{t}=c, X_{t-1}\neq c) = \sum_{t=1}^\infty t \sum_{s \neq c}P(X_{t}=c | X_{t-1} = s) P(X_{t-1}=s) $$ と書き表せます。\(P(X_{t}=c | X_{t-1} = s)=r_{sc}\)なので、\(P(X_{t-1}=s)\)を計算できれば期待値が評価できることが分かります。これはマルコフ連鎖で各時刻での状態の確率分布を求めることに対応します。
行列を使った期待値の計算(1)
マルコフ連鎖では遷移行列を使うことで、各時刻での分布\(P(X_t=s)\)を計算していくことができます。まず時刻\(t\)での確率分布をベクトル\(\pi_t \in [0,1]^{|\mathbb{S}|}\)で表現します。\(\pi_t\)は具体的には以下のように時刻\(t\)での各状態の確率を並べたものとなります: $$ \pi_t = [P(X_t=\phi(0)), P(X_t=\phi(1)), \cdots , P(X_t=c=\phi(|\mathbb{S}|-1))]. $$ この表現を使うと\(\pi_t\)は初期分布\(\pi_0\)を使い、以下のように書き表せます: $$ \pi_t =\pi_0 R^t. $$ ここで遷移行列\(R\)は\(n+1\)行\(m+1\)列成分に遷移確率\(r_{\phi(n)\phi(m)}\)を並べたものです。この\(\pi_t\)の表現を使うと期待値は以下のように計算されます: $$ S = \sum_{t=1}^\infty t\pi_0 R^{t-1}e. $$ ここで\(e\)はある状態\(s \neq c\)から状態\(c\)へ遷移する確率(\(r_{s c}\))を並べたベクトルです: $$ e=[r_{\phi(0)c}, r_{\phi(1)c}, \cdots , r_{\phi(|\mathbb{S}|-2)c}, 0]^T. $$ \(e\)を右からかけることは\(\sum_{s \neq c}P(X_{t}=c | X_{t-1} = s)\)での計算に対応しており、最後の成分が\(0\)なのは\(\sum_{s \neq c}\)が\(s=c\)の場合を除外していることに相当します。
行列を使った期待値の計算(2)
後々の議論のために、\(\sum_{t=1}^\infty t\pi_0 R^{t-1}e\)をさらに変形します。まず、\(R\)を以下のような部分行列に分解します: $$ \left[ {\begin{array}{cc}
Q & \eta \\
0 & 1 \\
\end{array} } \right]
= R. $$ ここで\(r_{cc}=1\)であることに注意してください。\(R^t\)に関して以下が成り立ちます: $$ R^t =
\left[ {\begin{array}{cc}
Q^t & * \\
0 & 1 \\
\end{array} } \right]. $$ \(e = [\eta^T, 0]^T\)である事に注意すると、期待値は最終的に以下のように計算できます: $$ S = \sum_{t=1}^\infty t\pi_0^\prime Q^{t-1}\eta. $$ ここで\(\pi_0^\prime \in \mathbb{R}^{|\mathbb{S}|-1}\)は\(\pi_0\)から末尾を除いたものです: $$ \left[ {\begin{array}{cc}
\pi_0^\prime & * \\
\end{array} } \right]= \pi_0. $$ 初期分布\(\pi_0\)及び\(\pi_0^\prime\)はどのような値でも良いのですが、「アイテムを持っていない状態から始めること」に相当する\(\pi_0 = [1, 0, \cdots, 0]\)を実装では採用しました。
無限級数の総和の評価方法
\(S = \sum_{t=1}^\infty t\pi_0^\prime Q^{t-1}\eta\)の計算方法について考えます。\(S\)は無限級数の総和なので(総和を途中で打ち切るなどの近似をしないと)このままでは数値的に評価できません。そのために問題を一般化してみて、適当な行列\(A\)に対して定義された以下のような級数和\(G(A)\)の計算方法を考えてみます: $$ G(A) = \sum_{n=1}^{\infty}nA^{n-1}. $$ この総和は行列\(A\)のレゾルベントを使うと計算することができることが分かります。
レゾルベントとは
行列(一般には線形作用素\(A\))に対して、レゾルベント\(R(z, A)\)は以下のように定義されます: $$ R(z, A)=(A-zI)^{-1}. $$ ここで\(z \in \mathbb{C}\)は(\(A\)が行列の場合は)\(z \in \{ z : \det(A-zI) \neq 0\}\)を満たす値です。さらに\(A\)のスペクトル半径)を\(\rho(A)\)として\(|z| > \rho(A)\)が満たされる時、以下のような級数和と等しくなります: $$ R(z, A) = \sum_{n=0}^{\infty} \frac{A^n}{z^{n+1}}. $$ この式は、スペクトル半径の性質から\(\lim_{n \to \infty} (A/z)^n = 0 \leftrightarrow |z| > \rho(A)\)が成り立つことに注意しつつ右辺に\((A-zI)\)をかけて具体的に計算してみることで証明できます。\(R(z, A)\)の級数和での表示はローラン級数展開の形になっており、従って\(R(z, A)\)は\(|z| > \rho(A)\)で正則なので、微分することができます。
\(R(z, A)\)微分して級数の評価に適用する
\(G(A)\)は\(R(z, A)\)の2つの表現での微分を考えることで計算できます。 まず、\( \sum_{n=0}^{\infty} A^n/z^{n+1}\)を微分して\(z=1\)を代入すると以下が得られます: $$ \left. \frac{\mathrm{d} R(z, A)}{\mathrm{d} z} \right|_{z=1} = \left. \frac{\mathrm{d}}{\mathrm{d} z} \sum_{n=0}^{\infty} \frac{A^n}{z^{n+1}} \right|_{z=1}
= – \sum_{n=0}^{\infty} (n+1)A^{n}. $$ ここで\(G(A)\)の定義と見比べてみると以下が分かります: $$ G(A) = \sum_{n=1}^{\infty} nA^{n}
= \sum_{n=0}^{\infty} (n+1)A^{n}
= – \left. \frac{\mathrm{d} R(z, A)}{\mathrm{d} z} \right|_{z=1}. $$ 同様にして\((A-zI)^{-1}\)の\(z=1\)での微分は逆行列の微分の公式 $$ \left. \frac{\mathrm{d}}{\mathrm{d} c}(A+ c B)^{-1}\right|_{c=0} = – A B A $$ を使うことで以下のように計算できます: $$ \left. \frac{\mathrm{d}}{\mathrm{d} z} (A-zI)^{-1}\right|_{z=1} = \left. \frac{\mathrm{d}}{\mathrm{d} z} (A-I – zI)^{-1}\right|_{z=0}
= (A-I)^{-2}. $$ 以上の2つの微分の結果を合わせると以下が得られます: $$ G(A) = – (A-I)^{-2}. $$ 無限級数の総和\(G\)を逆行列を使って表現することが出来ました。
\(S\)の評価に適用
以上の結果を使うことで\(S\)は以下のように計算できます: $$ S = \sum_{t=1}^\infty t\pi_0^\prime Q^{t-1}\eta = \pi_0^\prime\left( \sum_{t=1}^\infty t Q^{t-1} \right)\eta
= \pi_0^\prime G(Q) \eta = – \pi_0^\prime (Q-I)^{-2}\eta. $$ ここで\(\rho(Q) < 1\)が成り立っている必要があることに注意して下さい。\(R\)の場合だと\(\rho(R) =1\)となってしまい、このような議論を適用することはできません。期待値評価として、\(\sum_{t=1}^\infty t\pi_0 R^{t-1}e\)を使わなかったのはここに理由があります。\(\rho(Q) < 1\)が成り立っていることはおまけにて証明します。
\(- \pi_0^\prime (Q-I)^{-2}\eta\)はもう少し簡略化することができます。 \(e \in R^{|\mathbb{S}|-1}\)を\(e = [1, 1, \cdots, 1]^T\)とすると、\(R\)の各行の総和が\(1\)(遷移行列の性質より)であることから、\(e = Re = Qe + \eta \)が成り立ちます。ここから、\((I-Q)^{-1}\eta= e\)が得られ、これを使うと最終的に以下が得られます: $$ S = \pi_0^\prime (I-Q)^{-1}e. $$
実装にあたって
数値計算コード/Webアプリとして実装する際に行った工夫などについて簡単に紹介します。
疎行列表現
\(R\)や\(Q\)や\(I-Q\)は、殆どの成分が\(0\)の行列です。 このような行列は疎行列と呼ばれ、通常の行列よりも数値的に効率良く扱うことができます。Pythonの数値計算ライブラリであるSciPyにはscipy.sparseという疎行列専用のライブラリがあり、実装ではこれを用いました。
逆行列は計算したらダメ
逆行列の計算には\(O(N^3)\)の計算量が必要となります。 今回のケースの様に、もし必要な値が逆行列に何らかのベクトルをかけた結果なら、代わりに連立一次方程式を解く問題に置き換えることで計算量を\(O(N^2)\)まで抑えることが出来ます。具体的には、\(A^{-1}b\)を求めることは、以下の連立1次方程式を\(x\)について解くことと等価です: $$ Ax=b. $$ 疎行列が絡む連立一次方程式を解くには、例えばscipy.sparse.linalg.spsolveなどが使えます。
アプリとしてデプロイ
今回のアプリは最終的にはSPA(というほど大層なものではありませんが)の形でまとめました。 フロントエンドはVue.jsを使用しており、バックエンドはPython 3/Google App Engineを使用しています。
特にApp Engineはデプロイ等も簡単で、またSciPyの利用もテンプレート的なものが用意されていたので非常に楽でした。
おまけ
数値計算コードを素早く開発するには
今回作ったもののプロトタイプ(状態空間の圧縮表現を使っていないバーション)は約一日で完成させました。これまでの経験から、数値計算コードを素早く開発するには「デバッグ時間の最小化」が最も重要でありそのためには以下が有効であると考えています:
- テストを書く(Pythonのdoctestは簡単に使えて便利)
- assertionを使い防御的なプログラミングに徹する
- 別ルートで正解を計算しておいて、結果の正しさを検証できるようにしておく
\(\rho(Q) < 1\)であることの証明
\(\rho(Q) < 1 \leftrightarrow \lim_{n \to \infty } Q^n = 0\)及び適当な自然数\(k\)で\( \forall k > 0[\lim_{n \to \infty } Q^n = \lim_{n \to \infty} (Q^k)^n] \)が成り立つので、\( \forall k > 0 [ \rho(Q) < 1 \leftrightarrow \rho(Q^k) < 1]\)が言える。なので適当な\(k\)に関して\(\rho(Q^k) < 1\)が成り立つことを言えば良い。スペクトル半径は作用素ノルム(\(||\cdot||_{op}\))で上から押さえられるので、適当な\(k\)に関して\(||Q^k||_{op} < 1\)が言えれば充分である。\(L_1\)-ノルムから\(L_1\)-ノルムへの作用素ノルムを考える。\(Q\)は全ての成分が正なので全ての成分が正であるベクトル\(x\)に\(Q^k\)を作用させた時に、その\(L_1\)-ノルム\(||x^T Q^k||_1\)が\(||x||_1\)より小さくなくことを言えば良い。また\(x\)は特に、\(||x||_1=1\)の場合を考えれば充分である。つまり\(||x^T Q^k||_1 < 1\)を言えば良い。\(||x^T Q^k||_1\)は\(Q\)の構成法から、適当な初期分布(最初からアイテムコンプである確率は\(0\)として)から始めた時に、\(k\)ステップ後に「アイテムコンプ状態でない」確率を表す。なので、\(\forall n [p(n) > 0]\)より、どのような初期分布から始めても、適当な\(k\)を取れば\(||x^T Q^k||_1 < 1\)が成り立つ。
